Marginal Revenue Formula

Marginal Revenue Formula | What is Marginal Revenue?

Marginal Revenue Formula is the revenue that is gained from the sale of an additional unit. It is the revenue that a company can generate for each additional unit sold; there is a marginal cost attached to it, which is to be accounted for.

For example, Mr. A sells 50 packets of homemade chips every day and he incurs some cost to sell and produce them. He determined the price of each packet to be $5, adding all the cost and his profit, where his profit is $1.50 per packet. Now, Mr. A produced 55 packets one day by mistake and took all of them to the market. With no surprise, he was able to sell all 55 packets for $5 each. He made his usual $250 by selling 50 packets.

In addition to that, he sold 5 packets, which were produced by mistake. He was selling the packets for $5 and since he sold 5 additional packets, he had a Marginal Revenue of $25 ($5 x 5). This is how Marginal Revenue is calculated. It is dependent on supply and demand, and on the type of market as well, such as Perfect Competition and Monopoly.

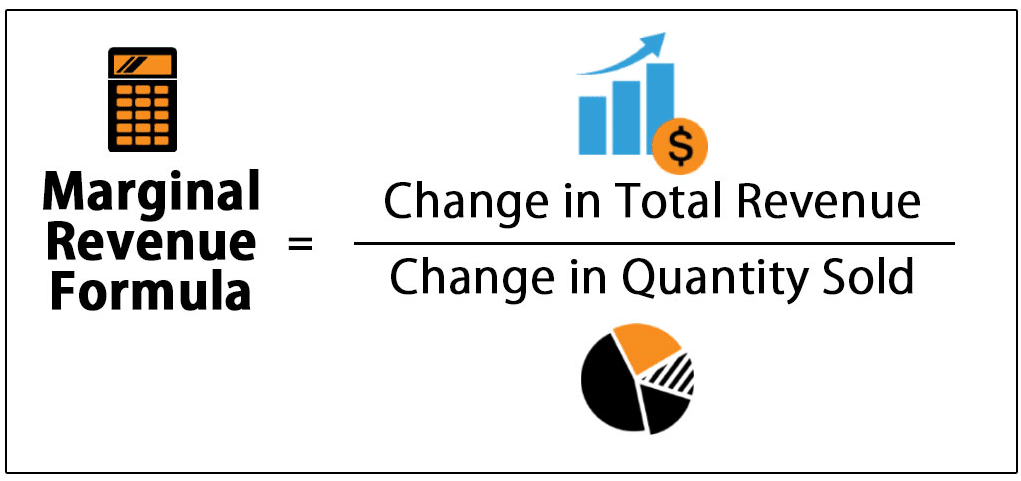
Marginal Revenue Product Formula | Formula For Marginal Revenue

The marginal revenue formula is calculated by dividing the change in total revenue by the change in quantity sold.

Marginal Revenue Formula Calculus

Jan’s Machining is a manufacturer of office supplies. Jan operates in an industry with several limited competitors and a set demand.

Jan figures that she can produce 100 pencils and sell them for $150 each resulting in $15,000 of revenues. Continuing with her analysis, Jan estimates that she will need to drop the price from $150 a pencil to $149 a pencil if she produces more than 2,000 units. Here’s how to find marginal revenue if Jan produced one extra unit.

Read Also: Double Declining Balance Depreciation

Since Jan had to drop her price $1 in order to produce and sell an extra unit, her revenue per unit went down, but her total revenues went up. Thus, Jan’s marginal revenue for this product is $49. We calculated that by multiplying the new production amount (2,001 units) by the new price ($149) and subtracting the original revenue number (2,000 units x $150 = $15,000).

This example can be expanded into different products, quantities, and industries, but we will keep it simple for now.

Marginal Revenue Formula Monopoly

As you can see from our example, the marginal revenue definition is a pretty simple concept. It does, however, have a huge influence over product pricing and production levels based on the manufacturer’s industry and product.

For instance, in a truly competitive market place where manufacturers are selling mass-produced, homogenous products at the market price, the marginal revenue is equal to the market price. In other words, manufacturers of commodities with little differentiation will always sell their products at the market price because it’s a competitive market place. If they raise their prices, consumers will buy from one of their competitors. You can think of this as a farmer who sells corn. The market sets the corn price each year. If he charges more than the market, consumers will purchase corn from his competitors because there is no difference between his product and theirs.

The opposite is true in low output or highly specialized industry. Since there are fewer product alternatives available, the production level of the company affects the selling price. In other words, less supply will increase demand and increase the willingness of consumers to pay higher prices. The company obviously has to keep the marginal revenue product inside the constraints of the price elasticity curve, but they can adjust their output and pricing structure to optimize its profitability.

Marginal Revenue Product Of Labor Formula

Marginal Revenue Curve

Let us examine the concept of Marginal Revenue in greater detail. The Marginal Cost curve is a “U” shape curve because the marginal cost for 1-5 additional units will be less and with more incremental units, the marginal cost will begin to rise. The Marginal Revenue curve is sloping downwards because, with one additional unit sold, we would generate revenue close to our normal revenue but as we start selling more and more, we would require reducing the price of the item we are selling. Otherwise, we will not be able to sell it, which is also known as the law of diminishing margin. So, the more you sell after a normal limit, the more the price will diminish and so will the revenue.

Average Revenue Curve

There is an Average Revenue curve or Demand curve, which is not the consumers’ demand curve but rather the producers’ demand curve. The curve represents the average quantity at an average price. Now that we understand what these curves are and what their function is, let us discuss marginal revenue in the context of marginal cost.

Let us say Mr. X is selling boxes of candy. He sells 25 boxes every day for $2 each and makes a profit of $0.50 on every box that he sells. Now, due to an increase in demand, he was able to sell 5 additional boxes of candy for the same price.

He incurred the same cost, which leaves him with the same amount of profit on these boxes as well, which will add up to $2.50 ($0.50 x 5).

Mr. X calculated that he could sell even more boxes of candy, so he ordered 10 more boxes. Now because of government restrictions and limited production, the cost of each box after the 30^th box increased by 10%, which made the 5 additional boxes of candy cost $1.65 each. His total cost = (30 boxes @ $1.50 = $45 and 5 boxes @ $1.65 = $8.25) total cost = $45 + $8.50 = $53.50.

Read Also: Retained Earnings Formula

Now he went to the market and tried to sell those candy boxes for the normal price of $2 each for the first 30 boxes and after that, he priced each box of candy for $2.15. He could sell 30 boxes easily and was not able to sell the remaining 5 boxes at the price he determined. In order to sell the remaining boxes, he needed to reduce the price to the normal price, otherwise, people would buy them from some other seller. He sold his remaining 5 boxes for $2 and had a diminishing marginal return on those 5 boxes. This is how marginal cost and diminishing marginal returns work with the marginal cost taken into account.